The commonly envisioned “world computer”—a globally distributed platform capable of handling all computational tasks and built on trust—is an invalid hypothesis. In fact, the future of Web3 will not be its outcome. This perspective stems from a profound insight into the nature of the Turing machine model: it is incomplete and can only function as a deterministic computational tool. Even with infinite performance scalability, such a “machine of trusted code” possesses only the capabilities of a tool and cannot construct a complex and non-deterministic system like the Bitcoin network. The key lies in the fact that trust does not originate from the deterministic, centralized “world computer” itself, but rather emerges from relative adaptation within asymmetric interactions.

The Boundary of “Turing Completeness” and the Necessity of the “Non-Computable”

The definition of “Turing completeness” is precisely limited: “Turing completeness is merely completeness over all that is defined as computable by Turing.” This is crucial. What the Turing machine and its derivative models can process are, in essence, problems that can be solved through finite steps and explicit rules—i.e., “computable” problems. However, many complex phenomena in the real world—especially those involving human behavior, social interaction, game-theoretic decisions, and unexpected events—often cannot be fully formalized into computable problems.

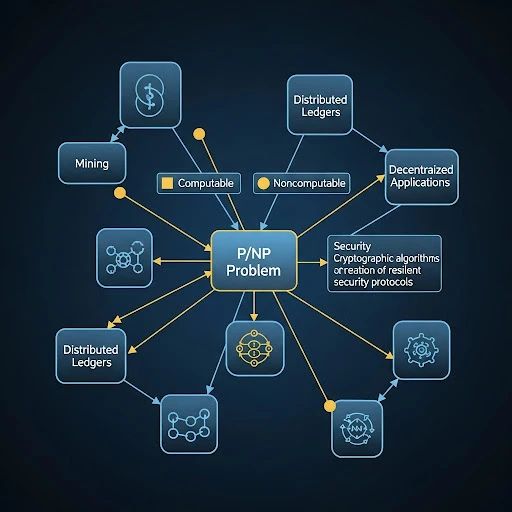
To achieve the completeness required for “adaptive complex systems,” we must transcend this purely “computable completeness” and attain “(computable + non-computable) completeness.” This implies that a truly robust, secure, and self-evolving system must not only efficiently process its internal deterministic computations, but also be able to somehow “handle” or “adapt to” those non-formalizable and non-exhaustive “non-computable” aspects.

The Direction of Exploring the “Non-Computable”: Asymmetric Interaction in P/NP

The direction of exploring the “non-computable” points toward the asymmetric interaction in the P/NP problem. In cryptography, public-key cryptography (asymmetric encryption) precisely leverages this computational asymmetry: encryption is easy (a P problem), while decryption is only easy if the private key is known—otherwise, it is extremely difficult (an NP problem). This “hard to compute” characteristic is the foundation of security.

In a complex system, this “non-computable” property is embodied through asymmetric interaction. The cost of attacking a system (which may involve solving a “non-computable” problem) is much higher than the cost of normal use and verification (solving a “computable” problem). It is this computational asymmetry that provides vital assurance for the system’s security and reliability.

Bitcoin: The First Artificial System with “(Computable + Non-Computable) Completeness”

Describing Bitcoin as “the first artificial adaptive system that satisfies (computable + non-computable) completeness” offers a new theoretical explanation for its success.

• Computable aspects: Bitcoin’s core operations—transaction verification, hash computation, block propagation—are all based on rigorous and predictable algorithms, representing classic “computable” tasks.
• Non-computable aspects (expressed through P/NP asymmetric interaction):
• – Emergence of the longest chain: The formation of Bitcoin’s longest chain is not a purely computational outcome, but the result of miner game-playing within the P/NP asymmetric interaction. Finding a valid hash is a “non-computable” problem (NP problem), while verifying it is “computable” (P problem). Miners’ competition in computing power, strategic choices, and expectations of future rewards all involve “non-computable” elements, eventually leading to the emergent consensus of the longest chain.
• – UTXO and human-machine interaction: Bitcoin’s UTXO (Unspent Transaction Output) model also reflects P/NP asymmetry and is closely tied to human-machine interaction. Generating a new UTXO (i.e., initiating a transaction) involves operations such as digital signatures and is relatively complex, whereas verifying the validity of a UTXO is relatively simple. Users interact with UTXOs through wallets and other tools, and this interaction itself contains “non-computable” factors such as subjective decision-making and risk preferences.

Looking Ahead

Therefore, if a “world computer” model cannot internally generate or effectively handle the “non-computable” characteristics that arise from asymmetric interactions, then it cannot truly build a Bitcoin-like network—nor can it claim theoretical universality. Bitcoin’s success lies in its transcendence of the computational boundaries of traditional Turing machines. It cleverly integrates computability and non-computability, achieving true security and adaptability.

The concepts of “adaptive completeness” and “relational conventions in asymmetric interaction” proposed by Geb.network provide an important theoretical framework for understanding the socio-technical properties of blockchains. This helps better design and evaluate future cryptocurrencies and Web3 applications, enabling them to truly address real-world problems and achieve practical implementation.