‍1. What is the “Completeness Problem”?

In formal logic, Gödel’s Incompleteness Theorems state: any sufficiently powerful and consistent formal system must be incomplete. This means there will inevitably exist propositions within the system that cannot be proven or disproven by its own logic — i.e., unavoidable paradoxes or self-reference problems.

In blockchain systems, this incompleteness manifests as a core governance dilemma: When multiple valid blocks appear at the same block height, how can the system select a single “correct” block solely through internal rules, without external intervention?

In other words, the completeness problem of blockchains can be defined as: Completeness Problem = How to resolve conflicting but valid branches (forks) purely within the system itself, without relying on external authority?

2. The Incompleteness of BFT Systems

In BFT (Byzantine Fault Tolerant) consensus systems (including Ethereum after its transition to PoS), this inherent incompleteness is especially evident:

• When multiple valid blocks appear at height n (i.e., a fork), the system lacks a purely internal and automated final arbitration logic.
• To resolve such divergence, BFT systems rely on:
  • Node voting, message passing, and game-theoretic convergence, hoping the network naturally leans toward one state.
  • In cases of persistent or severe conflict, final arbitration often falls to human intervention — such as core developers, foundations, or community social consensus.
    

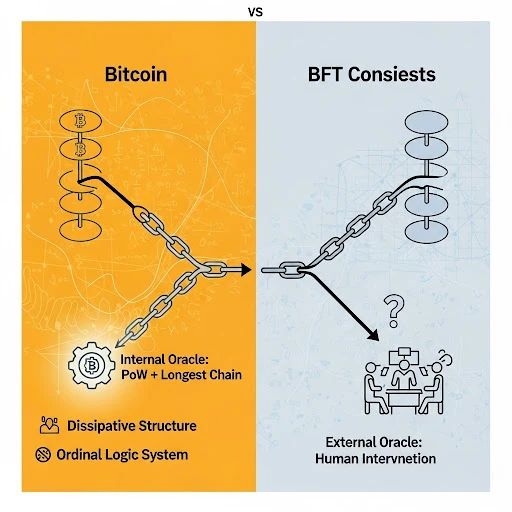
Conclusion: Incompleteness of BFT= At critical forks, the system cannot resolve conflicts endogenously or deterministically, requiring external “human intuition.”

This “intuition” resembles distributed neural resonance in the brain — consensus-forming but fundamentally an externalized oracle, not a native system component.

3. Bitcoin’s Completeness and Dissipative Structures

Bitcoin’s innovation lies in internalizing the arbitration mechanism for fork resolution directly into the protocol — via an automated oracle machine:

1. Nonce Resonance (PoW): Miners expend energy in massive parallel hash computations to find a random nonce. This process is akin to a dissipative structure in physics, where free particles (hash power) self-organize under energy input, emerging into ordered outcomes (valid blocks).‍
2. Longest Chain Rule: All nodes follow a clear rule: the chain with the greatest cumulative work (the longest chain) is the single valid history.
   

Here, the dissipative structure is the key abstraction:

• In physics, such structures are far-from-equilibrium open systems that consume energy continuously to generate stable order from chaos.
• In Bitcoin, PoW substitutes human intuition with physical energy dissipation — a de-humanized arbitration mechanism.

4. Ordinal Logic Systems: Ensuring Continuity

Resolving a single fork isn’t enough. A truly complete system must ensure infinite continuity, handling forks across the entire future evolution.

This requires the notion of an Ordinal Logic System:

• Turing Machine: Generates possibilities (miners producing candidate blocks).
• Oracle Machine: Selects a unique outcome (PoW + longest chain).
• Ordinal Logic: Ensures this generate–select cycle can iterate infinitely (transfinite iteration), producing an endless time series (the blockchain).
  

Thus, a complete blockchain system =Turing Machine (generation)+ Oracle Machine (selection)+ Ordinal Logic (continuity)

5. Comparative Table

6. Core Summary

• The completeness problem of Bitcoin: resolving the paradox of fork selection internally, while guaranteeing perpetual continuity.
• Bitcoin’s solution: an internalized dissipative oracle machine (PoW + longest chain) for automatic arbitration, plus ordinal logic transfinite iteration to ensure infinite evolution.
• BFT’s incompleteness: reliance on human intuition and external coordination for continuity and consensus.

Therefore, Bitcoin is not merely a distributed computing system or monetary network — it is a theoretically complete autonomous system, composed of Turing Machine (possibility) + Oracle Machine (conflict resolution) +Ordinal Logic (continuity).