We are standing at a critical turning point in computational theory — the notion of “computable” defined by the Turing Machine is no longer sufficient.

The future of computation will not be algorithmic computation, but structural computation.

I. The Origin of the Problem: The Boundary of the Turing Machine Is Being Broken

Traditional computational theory was founded by Turing. According to the definition of the Turing Machine:

• The formal system is closed
• The rules are deterministic
• The output is fully determined by the algorithm

Hence, mathematics and computer science drew a classic conclusion:

“Computable = What can be executed by a Turing Machine.”

However — this theory carries a hidden assumption: computation is single-machine and its structure remains unchanged.

But in the real world, computation has long surpassed this form:

• The Internet is computation
• Bitcoin is computation
• Distributed AI training networks are computation
• Self-organizing biological systems can be viewed as computation

All these systems consist of multiple computable units, yet their collective behavior lies beyond what a Turing Machine can describe.

Thus arises the question: When computable units form a network, is the whole still computable?

II. The Inspiration from Penrose Tiling: Local Symmetry Can Produce Global Irreducibility

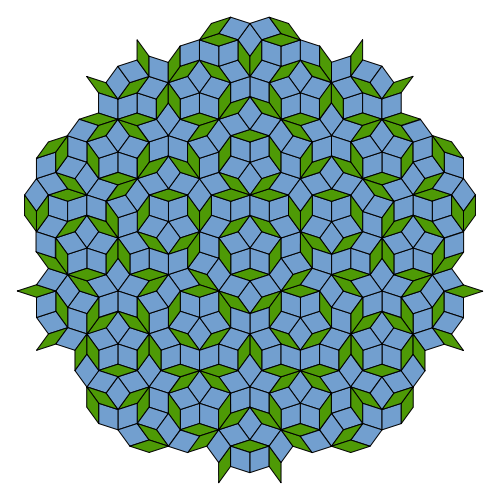
British mathematician Roger Penrose proposed a kind of aperiodic tiling (Penrose Tiling): It demonstrates an important phenomenon:

• Local rules are simple
• Unit shapes are symmetric

Yet the overall structure is non-periodic and irreducible. This reveals:

• Local determinacy ≠ Global determinacy
• Local rules ≠ Global behavior
• Local computability ≠ Global computability

This is a key insight for understanding Bitcoin, artificial intelligence, and self-organizing computation.

III. Turing Machines Can Combine into Non-Turing Machines

Imagine a network composed of multiple Turing Machine nodes:

• Each individual node is computable
• But once asynchronous competition, random delays, or local games occur between nodes
• The overall behavior may exhibit non-Turing properties

Therefore, we must acknowledge:

The combination of multiple Turing Machines does not equal a larger Turing Machine.

Structure transforms the very nature of computation.

IV. Redefining Computability: From “Algorithm” to “Structure”

We propose a new classification of computation:

\text{Computable}{Turing} \subset \text{Computable}{Structural}

In other words:

• Turing computation is only a subset of what is truly computable
• The real distributed world requires structural computability‍
• Bitcoin is the first engineering realization of structural computation

V. Why This Matters Profoundly

Redefining “computation” will:

• Advance the theory of decentralized systems
• Bridge artificial intelligence, self-organizing systems, and computational philosophy
• Even reshape future computational models and the foundations of mathematical logic