Most people understand Bitcoin from perspectives such as cryptography, economics, or computer science.

However, if we view it from the lens of mathematical philosophy and logic, we find that Bitcoin is actually a “hyper-formal system in reality”, integrating the Turing Machine, Oracle Machine, ordinal logic, and Nash game theory.

The philosophical prototype of this idea originates from the Taniyama–Shimura Conjecture (Modularity Theorem): Elliptic Curves ≡ Modular Forms

This equivalence not only led to the proof of Fermat’s Last Theorem, but also revealed a profound philosophical insight: equivalent systems can complement each other’s decidability.

The Logical Power of Parallel Formal Systems

Philosophical Interpretation: A single formal system cannot be completely self-consistent (Gödel’s Incompleteness Theorem), but when two equivalent systems interact, their overall ability to determine truth can be enhanced.

In other words, cross-system mapping is a craftsmanship for solving undecidable problems.

The Logical Equivalence Structure in Bitcoin

The same concept is realized within Bitcoin:

How Turing and Nash’s Parallel Logic Construct Bitcoin

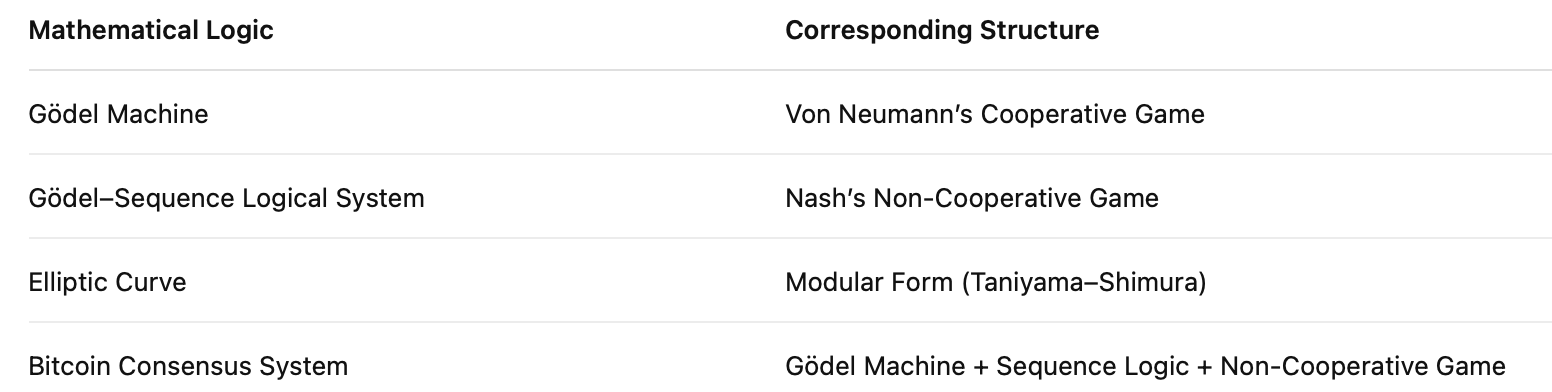
Core Mechanism Summary

• Turing’s Ordinal Logic → Builds Bitcoin’s formal structure and temporal order
• Longest Chain Rule → Implementation of ordinal logic through transfinite iteration
• PoW Hashrate Game → Realization of Nash’s non-cooperative game
• BTC Reward Model → Monotonic potential function ensuring convergence to a unique Nash equilibrium chain

Formal Expression

Turing Machine + Oracle Machine → A transfinite iterative ordinal logic system

• The Turing Machine provides computable consistency
• The Oracle Machine provides decision power beyond computability
  

Ordinal Logic System + Nash Non-Cooperative Game → A decentralized adaptive consensus mechanism

• The Ordinal Logic System provides temporal order and formal completeness
• The Non-Cooperative Game provides economic motivation and decentralized execution
  

Symbolic Representation: (Turing Machine + Oracle Machine) ⇒ Ordinal Logic System + Non-Cooperative Game ⟹ Decentralized Adaptive Consensus Mechanism

Philosophical Summary‍

The Taniyama–Shimura Conjecture tells us: Equivalent systems can complement decidability. Bitcoin proves:The parallel logic of Turing and Nash can form a hyper-formal system that achieves decentralized stable order.

• Turing Machine → Consistency
• Ordinal Logic → Scalability beyond Turing systems
• Non-Cooperative Game → Decentralization
• BTC Economic Model → Convergence

Bitcoin is the first system in human history that integrates these four layers of logic and operates them in the real world.