In traditional physics, time is often regarded as a symmetric and reversible mathematical parameter. However, in reality, complex systems invariably exhibit the irreversibility of time: waves dissipate, life ages, history never returns. As early as the late 19th century, Poincaré revealed the root of this irreversibility, laying profound groundwork for later understanding of electromagnetic waves, brain consciousness, NP problems, and cryptographic technology.

1. Poincaré’s Insight: Non-integrability and the Arrow of Time

Poincaré discovered in his study of dynamical systems that when a system is composed of multiple interacting free particles, it can no longer be described by integrable functions. The state evolution of the system no longer has a closed-form solution; its behavior exhibits high nonlinearity, chaos, and even sudden “jump-like” transitions.

What truly destroys “reversibility” is not kinetic energy itself, but the potential energy coupling between degrees of freedom.

These couplings produce resonance phenomena: when multiple particles (degrees of freedom) enter a certain frequency/phase-matching state, system-level coordinated changes are triggered. This resonance is nonlocal, emergent, and irreducible. It marks the critical point from integrable to non-integrable, from reversible to irreversible.

2. Electromagnetic Waves: Resonance Emergence in Non-integrable Fields

Electromagnetic waves are essentially a nonlinear, nonlocal, non-integrable wave field structure. During propagation, due to interference, superposition, and phase coupling, they often form certain instantaneous “bright spots” or “sudden structures” (such as Poisson bright spots), which cannot be reconstructed by local differentiation.

More critically:

• The field potential energy of electromagnetic waves is not a local quantity but the overall interference result of the system;
• Once resonance occurs, the system simultaneously triggers infinitesimal reactions across multiple dimensions;
• This “simultaneity” causes the system to suddenly transition from continuous evolution into an irreversible trajectory.
  

This perfectly aligns with Poincaré’s view that “potential energy coupling leads to irreversibility.”

3. The NP Problem: The Computational Mirror of Irreversibility

In computational theory, NP problems inherently display a form of asymmetric complexity:

• Solution verification is easy (low entropy, reversible)
• Solution searching is hard (high entropy, irreversible)
  

This means: the NP solving process = dissipating energy from a high-entropy space → constructing an ordered structure. Essentially, this is a computational version of a dissipative structure. The emergence of a solution often carries “jump-like” and “intuitive” characteristics, just like the resonance transitions in Poincaré’s dynamical systems.

The “irreducibility of solutions” in NP problems = the “irreversibility of states” in physical systems.

4. Bitcoin: Turning Irreversibility into Value

Bitcoin’s core mechanism — Proof of Work (PoW) — directly introduces NP problems into economic and information security systems:

1. The generation of each block is equivalent to solving an NP problem
2. The solving process consumes massive energy (electricity → hash computation)
3. Once confirmed on-chain, history cannot be tampered with
   

In other words: the Bitcoin blockchain = an “irreversible time structure” built through entropy dissipation. It is a machine that mints the directionality of time using energy. The growth of the structure strictly follows the “arrow of time” and cannot be rolled back.

5. The Brain, Consciousness, and the Emergence of the Sense of Time

In neural systems, the brain’s electromagnetic activity exhibits a non-integrable structure similar to Poincaré’s dynamical systems:

• Perception, intuition, and inspiration are not the results of linear computation
• They arise from sudden resonances between multiple free-degree brain regions
• Electromagnetic fluctuations form irreducible field structures
• Consciousness unfolds continuously within this structure in an irreversible manner over time
  

Consciousness is not an algorithm, but a stable self-referential dissipative resonance structure in time. Its essence is consistent with the suddenness of NP problem solving, the irreducibility of electromagnetic resonance.

6. A Unified Perspective: Irreversibility as the Price of Systemic Order‍

Bringing together the above phenomena yields the following cognitive framework:

Conclusion: Time is Not a Background, but an Emergence

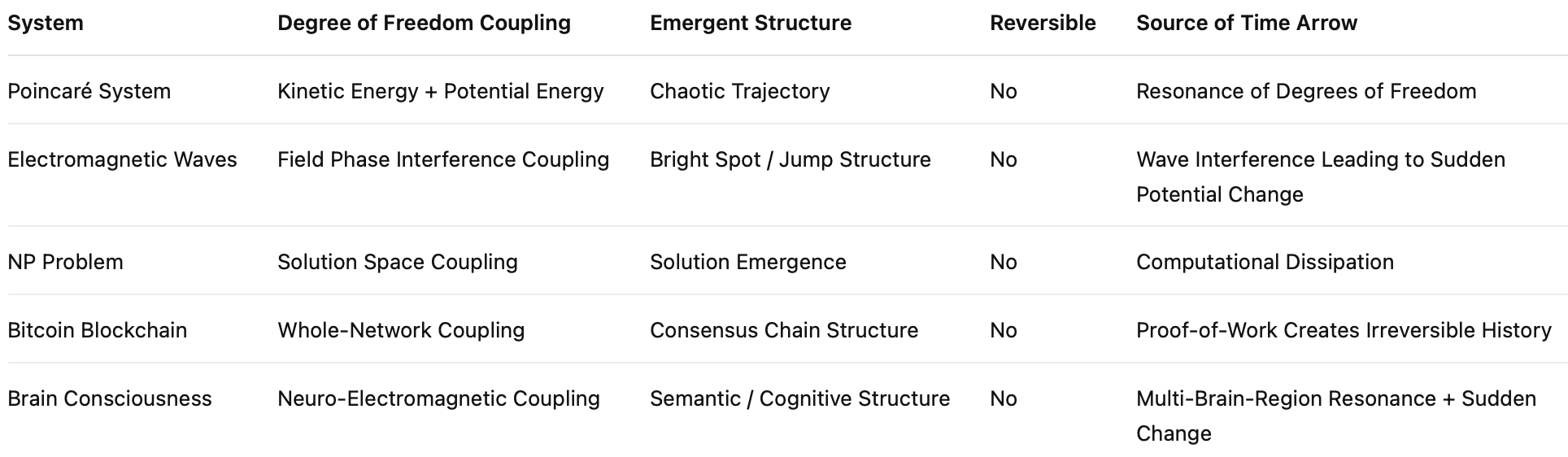
Time is not an inherent coordinate axis of the universe, but an irreducible process that naturally emerges from within a system when potential energy coupling, resonance, and non-integrable structures arise between its degrees of freedom.

Poincaré foresaw this long ago. Today, from electromagnetic waves, computational complexity, cryptocurrency, and consciousness studies, we once again return to this core question: irreversible time is the mother of all structures. Without emergence, there is no meaning; without irreversibility, there is no reality.